This prize was created on the initiative of Frank Callier, Professor Emeritus in the Department of Mathematics at UNamur, with a view to rewarding the excellence of a Master's thesis (120 credits) in Applied Mathematics at the University of Namur.
It rewards the quality of a research work in mathematics and its applications, which particularly stands out for its originality, the depth and rigor of its purpose, the scope of the results obtained and their applicability or publishability. Particular importance is attached to the candidates' personality, maturity, charisma, personal involvement in scientific work and ability to present results clearly and appropriately to a non-specialist audience.
Winner 2025: Edouard Bomans
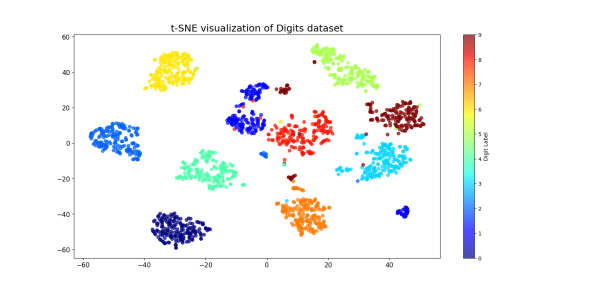
Title: Visualizing complex data: rethinking the distribution law of the t-SNE method
Promoter: Anne-Sophie Libert
Co-promoter: Benoît Frenay
Summary:
In my research dissertation, I chose to tackle a hypothesis that is rarely questioned in the scientific literature: the systematic use of Student's t law in the t-SNE algorithm, a method that is now a must for visualizing complex data. The aim of my work has been to reassess this fundamental choice, both theoretically and empirically, by questioning its validity and exploring alternatives potentially more suited to certain data structures.
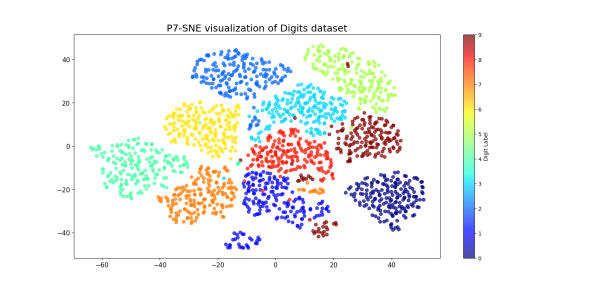
To this end, I have proposed replacing the t distribution with three other distributions with contrasting properties: the lognormal, the Pearson type VII and the Weibull distributions. These choices are not arbitrary: each modifies the forces of attraction and repulsion in the projected space in different ways, directly affecting the quality of the visualization obtained. I evaluated these modifications using three complementary metrics, on three well-known datasets: Iris, Digits and a subsample of MNIST. The results showed that some alternative parameterizations outperformed the classical version of t-SNE on several quantitative criteria. However, this work also highlighted a frequent mismatch between measured performance and perceived visual quality, underscoring the intrinsic complexity of visualization evaluation.
Another contribution of this dissertation lies in the fine-grained analysis of the forces underlying these methods. By modeling their radius of influence, I have highlighted that the classical version of t-SNE acts very locally, while the alternative distributions induce more global interactions. This structural difference could explain some of the observed variations in behavior, although a rigorous link between these forces and performance has yet to be established.